Array
C++에서 사이즈 구하기
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
1. 배열 회전 프로그램

기본적인 회전 알고리즘
temp를 활용해서 첫번째 인덱스 값을 저장 후 arr[0] ~ arr[n-1]을 각각 arr[1] ~ arr[n]의 값을 주고 arr[n]에 temp를 넣어준다.
void leftRotatebyOne(int arr[], int n){
int temp = arr[0], i;
for(i = 0; i < n-1; i++){
arr[i] = arr[i-1];
}
arr[i] = temp;
}
저글링 알고리즘 구현

최대공약수 gcd를 이용해 집합을 나누어 여러 요소를 한꺼번에 이동시키는 것
arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
1,2,3을 뒤로 옮길 때, 인덱스를 3개씩 묶고 회전시키는 방법
a) arr[] >> { 4 2 3 7 5 6 10 8 9 1 11 12}
b) arr[] >> { 4 5 3 7 8 6 10 11 9 1 2 12}
c) arr[] >> { 4 5 6 7 8 9 10 11 12 1 2 3}
역전 알고리즘 구현
회전시키는 수에 대해 구간을 나누어 reverse로 구현하는 방법
d = 2인 경우
1,2 / 3,4,5,6,7로 구간 나누기
첫번째 구간 reverse >> 2,1
두번째 구간 reverse >> 7,6,5,4,3
합치기 >> 2,1,7,6,5,4,3
합친 배열을 reverse >> 3,4,5,6,7,1,2
swap을 통한 reverse
void reverseOrder(int arr[], int start, int end){
while(start < end) {
int tmp = arr[start];
arr[start] = arr[end];
arr[end] = arr[start];
start++;
end--;
}
}
구간을 d로 나누었을 때 역전 알고리즘 구현
void rotateLeft(int arr[], int d, int n){
reverseArr(arr, 0, d - 1);
reverseArr(arr, d, n - 1);
reverseArr(arr, 0, n - 1);
}
2. 배열 특정 최대 합 구하기
arr[i]가 있을 때, i*arr[i]의 Sum이 가장 클 때 그 값을 출력하기
(회전하면서 최댓을 찾아준다.)
Input: arr[] = {1,20,2,10}
Output: 72
2번 회전시 아래와 같이 최댓값이 나온다.
{2, 10, 1, 20}
Input: arr[] = {10, 1, 2, 3, 4, 5, 6, 7, 8, 9}; Output: 330 9번 회전했을 때 아래와 같이 최대값이 나오게 된다.
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; 0*1 + 1*2 + 2*3 ... 9*10 = 330
접근 방법
arr[i]의 전체 합과 i * arr[i]의 전체 합을 저장할 변수 선언
최종 가장 큰 sum 값을 저장할 변수 선언
배열을 회전시키면서 i * arr[i]의 합의 값을 저장하고, 가장 큰 값을 저장해서 출력
해결법
회전 없이 i*arr[i]의 sum을 저장한 값 R0 = 0*arr[0] + 1*arr[1] +...+ (n-1)*arr[n-1]
1번 회전하고 i*arr[i]의 sum을 저장한 값
R1 = 0*arr[n-1] + 1*arr[0] +...+ (n-1)*arr[n-2]
이 두개를 빼면?
R1 - R0 = arr[0] + arr[1] + ... + arr[n-2] - (n-1)*arr[n-1]
2번 회전하고 i*arr[i]의 sum을 저장한 값
R2 = 0*arr[n-2] + 1*arr[n-1] +...+ (n-1)*arr[n-3]
1번 회전한 값과 빼면?
R2 - R1 = arr[0] + arr[1] + ... + arr[n-3] - (n-1)*arr[n-2] + arr[n-1]
여기서 규칙을 찾을 수 있음.
Rj - Rj-1 = arrSum - n * arr[n-j]
이를 활용해서 몇번 회전했을 때 최대값이 나오는 지 구할 수 있다.
3. 특정 배열을 arr[i] = i로 재배열 하기
ex) 주어진 배열에서 arr[i] = i 이 가능한 것만 재배열 시키기
Input : arr = {-1, -1, 6, 1, 9, 3, 2, -1, 4, -1}
Output : [-1, 1, 2, 3, 4, -1, 6, -1, -1, 9]
Input : arr = {19, 7, 0, 3, 18, 15, 12, 6, 1, 8, 11, 10, 9, 5, 13, 16, 2, 14, 17, 4}
Output : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
arr[i] = i가 없으면 -1로 채운다.
접근 방법
arr[i]가 -1이 아니고, arr[i]가 i가 아닐 때가 우선 조건
해당 arr[i] 값을 저장(x)해두고, 이 값이 x일때 arr[x]를 탐색
arr[x] 값을 저장(y)해두고, arr[x]가 -1이 아니면서 arr[x]가 x가 아닌 동안을 탐색
arr[x]를 x값으로 저장해주고, 기존의 x를 y로 수정
int fix(int A[], int len){
for(int i = 0; i < len; i++){
if(A[i] != -1 && A[i] != i){
int x = A[i];
while(A[x] != -1 && A[x] != x){
int y = A[x];
A[x] = x;
x = y;
}
A[x] = x;
if(A[i] != i){
A[i] = -1;
}
}
}
}
Linked List

연속적인 메모리 위치에 저장되지 않는 선형 데이터 구조
(포인터를 사용해서 연결)
각 노드는 데이터 필드와 다음 노드에 대한 참조를 포함하는 노드로 구성
Linked List를 사용하는 이유
배열은 비슷한 유형의 선형 데이터를 저장하는 데 사용할 수 있지만 제한 사항이 있다.
(1) 배열의 크기가 고정되어 있어 미리 요소의 수에 대해 할당을 받아야 한다.
(2) 새로운 요소를 삽입하는 것은 비용이 많이 든다.(공간을 만들고, 기존 요소 전부 이동)
장점
1. 동적 크기
2. 삽입/삭제 용이
단점
1. 임의로 액세스를 허용할 수 없다. 첫 번째 노드부터 순차적으로 요소에 액세스 해야한다. (이진 검색 불가능)
2. 포인터의 여분의 메모리 공간이 목록의 각 요소에 필요
노드 구현은 아래와 같이 데이터와 다음 노드에 대한 참조로 나타낸다.
struct Node {
int data;
struct Node *next;
}
SingleLinkedList
노드 3개를 잇는 코드 만들기
노드 추가
앞쪽에 노드 추가
void push(struct Node** head_ref, int new_data){
struct Node* new_node = (struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
특정 노드 다음에 추가
void insertAfter(struct Node* prev_node, int new_data){
if(prev_node == NULL){
printf("이전 노드가 NULL이 아니여야 합니다.");
return;
}
struct Node* new_node = (struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = prev_node->next;
prev_node->next = new_node;
}
끝쪽에 노드 추가
void append(struct Node** head_ref, int new_data){
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
struct Node *last = *head_ref;
new_node -> data = new_data;
new_node -> next = NULL;
if(*head_ref == NULL){
*head_ref = new_node;
return;
}
while(last->next != NULL){
last = last->next;
}
last->next = new_node;
return;
}
2024/05/18
Array vs ArrayList vs LinkedList
세개의 자료구조를 한 문장으로 정의하기
- Array는 index로 빠르게 값을 찾는 것이 가능
- LinkedList는 데이터의 삽입 및 삭제가 빠름
- ArrayList는 데이터를 찾는데 빠르지만, 삽입 삭제가 느림
자세한 비교
배열(Array)은 선언할 때 크기와 데이터 타입을 지정해야 한다.
int arr[10];
String arr[5];
array는 메모리 공간에 할당할 사이즈를 미리 정해놓고 사용하는 자료구조다.
계속 데이터가 늘어날 때, 최대 사이즈를 알 수 없을 때는 사용하기에 부적합하다.
중간에 데이터를 삽입하거나 삭제할 때도 매우 비효율적이다.
4번째 index 값에 새로운 값을 넣어야 할 경우, 원래값을 뒤로 밀어내고 해당 index에 덮어씌워야 한다.
size를 정해 놓은 배열에서는 해결하기엔 부적합한 점이 많다.
배열을 사용하면 index가 존재하기 때문에 위치를 바로 알 수 있어 검색에 편한 장점이 있다.
배열의 단점을 해결하기 위해 나온 것이 List다.
List는 array처럼 크기를 정해주지 않아도 된다. array에서 index가 중요하다면, List에서는 순서가 중요하다.
크기가 정해져있지 않기 때문에, 중간에 데이터를 추가하거나 삭제하더라도 array에서 갖고 있던 문제점을 해결 가능하다.
index를 가지고 있으므로 검색도 빠르다.
중간에 데이터를 추가 및 삭제할 때 시간이 오래 걸리는 단점이 존재한다.
(데이터를 추가하거나 삭제할때마다 줄줄이 당겨지거나 밀려날 때 진행되는 연산이 추가, 메모리 낭비 발생)
LinkedList란?
연결리스트에는 단일, 다중 등 여러가지가 존재한다.
종류가 무엇이든, 한 노드에 연결될 노드의 포인터 위치를 가리키는 방식으로 되어 있다.
단일은 뒤에 노드만 가리키고, 다중은 앞뒤 노드를 모두 가리키는 차이
이러한 방식을 활용하면서, 데이터의 중간에 삽입 및 삭제를 하더라도 전체를 돌지 않아도 이전 값과 다음값이 가르켰던 주소값만 수정하여 연결시켜주면 되기 때문에 빠르게 진행할 수 있다.
가장 좋은 방법 같아보이지만, List의 k번째 값을 찾아라에서는 비효율적이다.
array나 arrayList index를 갖고 있으므로 검색이 빠르지만, LinkedList는 처음부터 순차적으로 찾아야하므로 검색에 있어서는 시간이 더 걸린다는 단점이 존재한다.
스택 & 큐
스택(Stack)
입력과 출력이 한 곳(방향)으로 제한
LIFO(Last in First Out, 후입 선출): 가장 나중에 들어온 것이 가장 먼저 나옴
언제 사용하는가?
함수의 콜스택, 문자열 역순 출력, 연산자 후위표기법
데이터 넣기: push()
데이터 최상위 값 빼기: pop()
비어있는지 확인하기 : isEmpty()
꽉차있는지 확인하기 : isFull()
push와 pop할 때는 해당 위치를 알고 있어야 하므로 기억하고 있는 '스택 포인터(SP)'가 필요하다.
스택 포인터는 다음 값이 들어갈 위치를 가리키고 있다.(처음 기본값 -1)
private int sp = -1;
push
public void push(Object o){
if(isFull(o)){
return;
}
stack[++sp] = o;
}
스택 포인터가 최대 크기와 같으면 return
아니면 스택의 최상위 위치에 값을 넣는다.
pop
public Object pop(){
if(isEmpty(sp)){
return null;
}
Object o = stack[sp--];
return o;
}
스택 포인터가 0이 되면 null로 return;
아니면 스택의 최상위 위치 값을 꺼내온다.
isEmpty
private boolean isEmpty(int cnt){
return sp == -1 ? true: false;
}
입력 값이 최초 값과 같다면 true, 아니면 false
isFull
private boolean isFull(int cnt){
return sp + 1 == MAX_SIZE ? true : false;
}
스택 포인터 값 + 1이 MAX_SIZE와 같으면 true, 아니면 false
동적 배열 스택
위의 방식대로 구현하려면 스택에는 MAX_SIZE라는 최대 크기가 존재해야 한다.
(스택 포인터와 MAX_SIZE를 비교해서 isFull 메소드로 비교해야 되기 때문에)
최대 크기가 없는 스택을 만들려면?
arraycopy를 활용한 동적배열 사용
public void push(Object o){
if(isFull(sp)){
Object[] arr = new Object[MAX_SIZE * 2];
System.arraycopy(stack, 0, arr, 0 MAX_SIZE);
stack = arr;
MAX_SIZE *= 2;
}
stack[sp++] = o;
}
기존 스택의 2배 크기만큼 임시 배열(arr)을 만들고
arraycopy를 통해 stack의 인덱스 0부터 MAX_SIZE만큼을 arr배열의 0번째 부터 복사한다.
복사 후에 arr의 참조값을 stack에 덮어씌운다.
마지막으로 MAX_SIZE의 값을 2배로 증가시켜주면 된다.
이런경우, 스택이 가득찼을 때 자동으로 확장되는 스택을 구현할 수 있다.
스택을 연결리스트로 구현해도 해결 가능
public class Node {
public int data;
public Node next;
public Node(){
}
public Node(int data){
this.data = data;
this.next = null;
}
}
public class Stack {
private Node head;
private Node top;
public Stack(){
head = top = null;
}
private Node createNode(int data){
return new Node(data);
}
private boolean isEmpty(){
return top == null ? true: false;
}
public void push(int data){
if(isEmpty()){
head = createNode(data);
top = head;
}else {
Node pointer = head;
while(pointer.next != null){
pointer = pointer.next;
}
pointer.next = createNode(data);
top = pointer.next;
}
}
}
public int pop(){
int popData;
if(!isEmpty()){
popData = top.data;
Node pointer = head;
if(head == top){
head = top = null;
}else {
while(pointer.next != top){
pointer = pointer.next;
}
pointer.next = null;
top = pointer;
}
}
return popData;
}
return -1;
}
큐(Queue)
입력과 출력을 한 쪽 끝(front, rear)으로 제한
FIFO(First in First Out, 선입선출) : 가장 먼저 들어온 것이 가장 먼저 나옴
언제 사용하는가?
버퍼, 마구 입력된 것을 처리하지 못하고 있는 상황, BFS
큐의 가장 첫 원소를 front, 끝 원소를 rear라고 부른다.
큐는 들어올 때 rear로 들어오지만, 나올 때는 front부터 빠지는 특성을 가진다.
접근방법은 가장 첫 원소와 끝 원소로만 가능
데이터 넣기: enQueue()
데이터 빼기: deQueue()
비어있는 지 확인: isEmpty()
꽉차있는 지 확인: isFull()
데이터를 넣고 뺄 때 해당 값의 위치를 기억해야 한다.(스택에서 스택 포인터와 같은 역할)
이러한 위치를 기억하고 있는 것이 front와 rear이다.
front: deQueue할 위치 기억
rear: enQueue할 위치 기억
기본값
private int size = 0;
private int rear = -1;
private int front = -1;
Queue(int size) {
this.size = size;
this.queue = new Object[size];
}
2024/05/20
enQueue
public void enQueue(Object o) {
if(isFull()) {
return;
}
queue[++rear] = o;
}
enQueue 시, 가득 찼다면 꽉 차 있는 상태에서 enQueue를 했기 때문에 overflow
아니면 rear에 값 넣고 1 증가
deQueue
public Object deQueue(Object o) {
if(isEmpty()) {
return null;
}
Object o = queue[front];
queue[front++] = null;
return o;
}
deQueue를 할 때 공백이면 underflow
front에 위치한 값을 object에 꺼낸 후, 꺼낸 위치는 null로 채워줌
isEmpty
public boolean isEmpty() {
return front == rear;
}
front와 rear가 같아지면 비어진 것
isFull
public boolean isFull() {
return (rear == queueSize-1);
}
rear가 사이즈-1과 같아지면 가득찬 것
일반 큐의 단점 : 큐에 빈 메모리가 남아 있어도, 꽉 차있는것으로 판단할 수도 있음
(rear가 끝에 도달했을 때)
이를 개선한 것이 '원형 큐'
논리적으로 배열의 처음과 끝이 연결되어 있는 것으로 간주함!
원형 큐는 초기 공백 상태일 때 front와 rear가 0
공백, 포화 상태를 쉽게 구분하기 위해 자리 하나를 항상 비워둠
(index + 1) % size로 순환시킨다
기본값
private int size = 0;
private int rear = 0;
private int front = 0;
Queue(int size) {
this.size = size;
this.queue = new Object[size];
}
enQueue
public void enQueue(Object o) {
if(isFull()) {
return;
}
rear = (++rear) % size;
queue[rear] = o;
}
enQueue 시, 가득 찼다면 꽉 차 있는 상태에서 enQueue를 했기 때문에 overflow
deQueue
public Object deQueue(Object o) {
if(isEmpty()) {
return null;
}
preIndex = front;
front = (++front) % size;
Object o = queue[preIndex];
return o;
}
deQueue를 할 때 공백이면 underflow
isEmpty
public boolean isEmpty() {
return front == rear;
}
front와 rear가 같아지면 비어진 것
#sFull
public boolean isFull() {
return ((rear+1) % size == front);
}
rear+1%size가 front와 같으면 가득찬 것
원형 큐의 단점 : 메모리 공간은 잘 활용하지만, 배열로 구현되어 있기 때문에 큐의 크기가 제한
이를 개선한 것이 '연결리스트 큐'
#연결리스트 큐는 크기가 제한이 없고 삽입, 삭제가 편리
enqueue 구현
public void enqueue(E item) {
Node oldlast = tail; // 기존의 tail 임시 저장
tail = new Node; // 새로운 tail 생성
tail.item = item;
tail.next = null;
if(isEmpty()) head = tail; // 큐가 비어있으면 head와 tail 모두 같은 노드 가리킴
else oldlast.next = tail; // 비어있지 않으면 기존 tail의 next = 새로운 tail로 설정
}
- 데이터 추가는 끝 부분인 tail에 한다.
- 기존의 tail는 보관하고, 새로운 tail 생성
- 큐가 비었으면 head = tail를 통해 둘이 같은 노드를 가리키도록 한다.
- 큐가 비어있지 않으면, 기존 tail의 next에 새로만든 tail를 설정해준다.
dequeue 구현
public T dequeue() {
// 비어있으면
if(isEmpty()) {
tail = head;
return null;
}
// 비어있지 않으면
else {
T item = head.item; // 빼낼 현재 front 값 저장
head = head.next; // front를 다음 노드로 설정
return item;
}
}
- 데이터는 head로부터 꺼낸다. (가장 먼저 들어온 것부터 빼야하므로)
- head의 데이터를 미리 저장해둔다.
- 기존의 head를 그 다음 노드의 head로 설정한다.
- 저장해둔 데이터를 return 해서 값을 빼온다.
이처럼 삽입은 tail, 제거는 head로 하면서 삽입/삭제를 스택처럼 O(1)에 가능하도록 구현이 가능하다.
힙(Heap)
알아야할 것
1.힙의 개념
2.힙의 삽입 및 삭제
힙은, 우선순위 큐를 위해 만들어진 자료구조다.
먼저 우선순위 큐에 대해서 간략히 알아보자
우선순위 큐 : 우선순위의 개념을 큐에 도입한 자료구조
데이터들이 우선순위를 가지고 있음. 우선순위가 높은 데이터가 먼저 나감
스택은 LIFO, 큐는 FIFO
언제 사용하는가?
시뮬레이션 시스템, 작업 스케줄링, 수치해석 계산
우선순위 큐는 배열, 연결리스트, 힙으로 구현 (힙으로 구현이 가장 효율적!)
힙 → 삽입 : O(logn) , 삭제 : O(logn)
힙(Heap)
완전 이진 트리의 일종
여러 값 중, 최대값과 최소값을 빠르게 찾아내도록 만들어진 자료구조
반정렬 상태
힙 트리는 중복된 값 허용 (이진 탐색 트리는 중복값 허용X)
힙 종류
최대 힙(max heap)
부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
최소 힙(min heap)
부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리

구현
힙을 저장하는 표준적인 자료구조는 배열
구현을 쉽게 하기 위해 배열의 첫번째 인덱스인 0은 사용되지 않음
특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않음
(ex. 루트 노드(1)의 오른쪽 노드 번호는 항상 3)
부모 노드와 자식 노드 관계
왼쪽 자식 index = (부모 index) * 2
오른쪽 자식 index = (부모 index) * 2 + 1
부모 index = (자식 index) / 2
힙의 삽입
1.힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 삽입
2.새로운 노드를 부모 노드들과 교환
최대 힙 삽입 구현
void insert_max_heap(int x) {
maxHeap[++heapSize] = x;
// 힙 크기를 하나 증가하고, 마지막 노드에 x를 넣음
for( int i = heapSize; i > 1; i /= 2) {
// 마지막 노드가 자신의 부모 노드보다 크면 swap
if(maxHeap[i/2] < maxHeap[i]) {
swap(i/2, i);
} else {
break;
}
}
}
부모 노드는 자신의 인덱스의 /2 이므로, 비교하고 자신이 더 크면 swap하는 방식
2024/05/21
힙의 삭제
1. 최대 힙에서 최대값은 루트 노드이므로 루트 노드가 삭제된다. (최대 힙에서 삭제 연산은 최댓값 요소를 삭제하는 것)
2. 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
3. 힙을 재구성
int delete_max_heap(){
if(heapSize == 0){
return 0;
}
int item = maxHeap[1]; // 루트 노드의 값을 저장
maxHeap[1] = maxHeap[heapSize]; // 마지막 노드 값을 루트로 이동
maxHeap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드 0 초기화
for(int i = 1; i * 2 <= heapSize;) {
if(maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2+1]){
break;
}
else if(maxHeap[i*2] > maxHeap[i*2+1]){
swap(i,i*2);
i = i*2
}
else {
swap(i, i*2);
i = i*2+1;
}
}
return item;
}
Tree
Node와 Edge로 이루어진 자료구조
Tree 특성 이해하기

트리는 값을 가진 노드(Node)와 노드들을 연결해주는 간선(Edge)로 이루어진다.
그림에서 데이터 1을 가진 노드가 루트(Root)노드이다.
모든 노드들은 0개 이상의 자식 노드를 갖고 있고, 부모-자식 관계로 부른다.
트리의 특징
- 트리에는 사이클이 존재할 수 없다.(사이클이 만들어진다면, 트리가 아니고 그래프다)
- 모든 노드는 자료형으로 표현이 가능하다.
- 루트에서 한 노드로 가는 경로는 유일한 경로 뿐이다.
- 노드의 개수가 N개면, 간선은 N-1개다.
그래프와 트리의 차이는 사이클의 유무로 설명할 수 있다.
트리 순회 방식
트리를 순회하는 방식은 4가지가 존재한다.

1. 전위 순위(pre-order)
각 루트(Root)를 순차적으로 먼저 방문하는 방식
(Root >> 왼쪽 >> 오른쪽)
[1 > 2 > 4 > 8 > 9 > 5 > 10 > 11 > 3 > 6 > 13 > 7 > 14
2. 중위 순위(in-order)
왼쪽 하위 트리를 방문 후 루트(Root)를 방문하는 방식
(왼쪽 >> Root >> 오른쪽)
[ 8 > 4 > 9 > 2 > 10 > 5 > 11 > 1 > 6 > 13 > 3 > 14 > 7 ]
3. 후위 순위(post-order)
왼쪽 하위 트리부터 하위를 모두 방문 후 루트(Root)를 방문하는 방식
(왼쪽 >> 오른쪽 >> Root)
[ 8 > 9 > 4 > 10 > 11 > 5 > 2 >13 > 6 > 14 > 7 > 3 > 1 ]
4. 레벨 순회(level-order)
루트(Root)부터 계층 별로 방문하는 방식
[1 > 2 > 3 > 4 > 5 > 6 > 7 > 8 > 9 > 10 > 11 > 12 > 13 > 14]
Code
public class Tree<T> {
private Node<T> root;
public Tree(T rootData){
root = new Node<T>();
root.data = rootDat;
root.chldren = new ArrayList<Node<T>>();
}
public static class Node<T>{
private T data;
private Node<T> parent;
private List<Node<T>> children;
}
}
이진탐색트리(Binary Search Tree)
이진 탐색 트리의 목적?
이진 탐색 + 연결 리스트
이진탐색 : 탐색에 소요되는 시간복잡도는 O(logN), 삽입, 삭제가 불가능
연결리스트: 삽입, 삭제의 시간복잡도는 O(1), 탐색하는 시간복잡도가 O(N)
이 두가지의 장점을 모두 얻기 위함이 이진 탐색 트리
효율적인 탐색 능력을 가지고, 자료의 삽입 삭제도 가능하게 하기

특징
- 각 노드의 자식이 2개 이하
- 각 노드의 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 크다.
- 중복된 노드가 없어야 한다.
중복이 없어야 하는 이유?
검색 목적 자료구조에서 굳이 중복이 많은 경우에 트리를 사용해서 검색 속도를 느리게 할 필요가 없다.(트리에 삽입하는 것보다, 노드에 count 값을 가지게 하여 처리하는 것이 훨씬 효율적이다.)
이진탐색트리의 순회는 중위순회 방식(왼쪽 - 루트 - 오른쪽)
중위 순회로 정렬된 순서를 읽을 수 있다.
BST 핵심 연산
- 검색
- 삽입
- 삭제
- 트리 생성
- 트리 삭제
시간 복잡도
- 균등 트리: 노드 개수가 N개일 때 O(logN)
- 편향 트리: 노드 개수가 N개일 때 O(N)
삽입, 검색, 삭제 시간복잡도는 트리의 Depth에 비례
삭제의 3가지 Case
- 자식이 없는 leaf 노드일 때 >> 그냥 삭제
- 자식이 1개인 노드일 때 >> 지워진 노드에 자식 올리기
- 자식이 2개인 노드일 때 >> 오른쪽 자식 노드에서 가장 작은 값 or 왼쪽 자식 노드에서 가장 큰 값 올리기
편향된 트리(정렬된 상태 값을 트리로 만들면 한쪽으로만 뻗게된다.)는 시간복잡도가 O(N)이므로 트리를 사용할 여유가 사라진다.
>> 이것을 바로 잡도록 도와주는 개선된 트리가 AVL Tree, RedBlack Tree
해시(Hash)
데이터를 효율적으로 관리하기 위해, 임의의 길이 데이터를 고정된 길이의 데이터로 매핑하는 것
해시 함수를 구현하여 데이터 값을 해시 값으로 매핑한다.
Lee >> 해싱함수 >> 5
Kim >> 해싱함수 >> 3
Park >> 해싱함수 >> 2
...
Chun >> 해싱함수 >> 5 // Lee와 해싱값 충돌
데이터가 많아지면, 다른 데이터가 같은 해시 값을 충돌나는 현상이 발생하게 된다. 'collision 현상'
해시테이블을 쓰는 이유?
적은 자원으로 많은 데이터를 효율적으로 관리하기 위해
하드디스크나, 클라우드에 존재하는 무한한 데이터들을 유한한 개수의 해시값으로 매핑하면 작은 메모리로도 프로세스 관리가 가능해진다.
- 언제나 동일한 해시값 리턴, index를 알면 빠른 데이터 검색이 가능
- 해시테이블의 시간복잡도 O(1)
- 이진 탐색 트리의 시간 복잡도 O(logN)
충돌 문제 해결하는 방법
1. 체이닝: 연결리스트로 노드를 계속 추가해나가는 방식(제한 없이 계속 연결 가능, 메모리 문제)
2. Open Addressing: 해시 함수로 얻은 주소가 아닌 다른 주소에 데이터를 저장할 수 있도록 허용(해당 키 값에 저장되어있으면 다음 주소에 저장)
3. 선형 탐사: 정해진 고정 폭으로 옮겨 해시값의 중복을 피함
4. 제곱 탐사: 정해진 고정 폭을 제곱수로 옮겨 해시값의 중복을 피함
2024/05/23
트라이(Trie)
문자열에서 검색을 빠르게 도와주는 자료구조
정수형에서 이진탐색 트리를 이용하면 시간복잡도 O(logN)
하지만 문자열에서 적용했을 때, 문자열 최대 길이가 M이면 O(M*logN)이 된다.
트라이 활용하면? >> O(M)으로 문자열 검색이 가능!
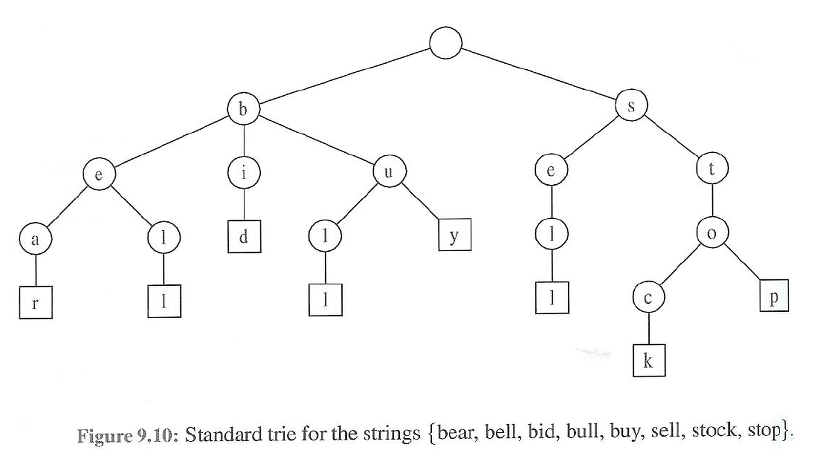
배열의 총 문자열 개수는 8개인데, 트라이을 활용한 트리에서도 마지막 끝나는 노드마다 '네모' 모양으로 구성된 것을 확인하면 총 8개가 존재한다.
Trie를 java로 구현한 코드
static class Trie {
boolean end;
boolean pass;
Trie[] child;
Trie(){
end = false;
pass = false;
child = new Trie[10];
}
public boolean insert(String str, int idx){
if(end) return false;
if(idx == str.length()){
end = true;
if(pass) return false;
else return true;
}else {
int next = str.charAt(idx) - '0';
if(child[next] == null){
child[next] = new Trie();
pass = true;
}
return child[next].insert(str, idx+1);
}
}
}
B Tree & B + Tree
이진 트리는 하나의 부모가 두 개의 자식밖에 가지질 못하고, 균형이 맞지 않으면 검색 효율이 선형검색 급으로 떨어진다.
이진 트리 구조의 간결함과 균형만 맞으면 검색, 삽입, 삭제 모두 O(logN)의 성능을 보이는 장점이 있다.
B Tree
DB, 파일 시스템에서 널리 사용되는 트리 자료구조의 일종이다.
이진 트리를 확장해서, 더 많은 수의 자식을 가질 수 있게 일반화 시킨 것이 B-Tree
자식 수에 대한 일반화를 진행하면서, 하나의 레벨어 더 저장되는 것 뿐만 아니라 트리의 균형을 자동으로 맞춰주는 로직까지 갖춘다.
단순하고 효율적이며, 레벨로 따지면 완전히 균형을 맞춘 트리이다.
대량의 데이터를 처리해야 할 때, 검색 구조의 경우 하나의 노드에 많은 데이터를 가질 수 있다는 점은 상당히 큰 장점이다.
대량의 데이터는 메모리보다 블럭 단위로 입출력하는 하드디스크 or SSD에 저장해야 하므로
ex) 한 블럭이 1024 바이트면, 2바이트를 읽으나 1024바이트를 읽으나 똑같은 입출력 비용 발생, 하나의 노드를 모두 1024바이트로 꽉 채워서 조절할 수 있으면 입출력에 있어서 효율적인 구성을 갖출 수 있다.
규칙
- 노드의 자료수가 N이면, 자식 수는 N+1
- 각 노드의 자료는 정렬된 상태
- 루트 노드는 적어도 2개 이상의 자식 노드를 가진다.
- 루트 노드를 제외한 모든 노드는 적어도 M/2개의 자료를 가지고 있어야 한다.
- 외부 노드로 가는 경로의 길이는 모두 같다.
- 입력 자료는 중복될 수 없다.
차수 M: B-트리의 차수 M은 한 노드가 가질 수 있는 최대 자식 수
B + Tree
데이터의 빠른 접근을 위한 인덱스 역할만 하는 비단말 노드(not Leaf)가 추가로 있다.
(기존의 B-Tree와 데이터의 연결리스트로 구현된 색인구조)
B-Tree의 변형 구조로, index 부분과 leaf노드로 구성된 순차 데이터 부분으로 이루어진다. 인덱스 부분의 key 값은 leaf에 있는 key 값을 직접 찾아가는데 사용한다.
장점
블럭 사이즈를 더 많이 이용할 수 있다.(key 값에 대한 액세스 주소가 없기 때문에)
leaf 노드끼리 연결 리스트로 연결되어 있어서 범위 탐색에 매우 유리하다.
단점
B-tree의 경우 최상 케이스에서는 루트에서 끝날 수 있지만, B+tree는 무조건 leaf 노드까지 내려가봐야 한다.
B-Tree & B+ Tree
B-Tree는 각 노드에 데이터가 저장된다.
B+Tree는 index 노드와 leaf 노드로 분리되어 저장된다.
(leaf 노드는 서로 연결되어 있어서 임의접근이나 순차접근 모두 성능이 우수하다.)
B-Tree는 각 노드에서 key와 data 모두 들어갈 수 있고, data는 disk block으로 포인터가 될 수 있다.
B+Tree는 각 노드에서 key만 들어간다. data는 모두 leaf 노드에만 존재한다.
B+tree는 add와 delete가 모두 leaf 노드에서만 이루어진다.
'Backend > CS' 카테고리의 다른 글
| [기술면접대비 CS전공 핵심 요약집] 운영체제 (0) | 2024.05.17 |
|---|---|
| [Tech Interview] Network (0) | 2024.05.08 |
| [면접을 위한 CS 전공지식 노트] 운영체제 (2) | 2024.03.29 |
| TCP, UDP (1) | 2024.01.04 |
| IP(인터넷 프로토콜) (0) | 2024.01.04 |



