나를 돌아보기
오늘은 기상을 좀 늦게했다. 아직 온전히 내 공부에 집중하기엔 방해되는 요소들이 너무 많다. 특히 휴대폰이 너무나 방해가 된다. 수시로 카톡과 인스타에 들락날락한다. 온전히 몰입해도 부족한 상황 가운데 몰입을 방해하는 요소들로 인해 몰입을 하지 못하는 것 같다. 이 몰입을 방해하는 요소들을 전부 내려놓기위해 오늘 아침에 인스타그램을 삭제했고, 카톡 또한 밥먹는 시간 외에는 보지 않으려고 한다. 오늘 아침에 신앙 서적에서 읽은 책의 내용이 너무 감명깊었다. 내용은 다음과 같다. 하나님은 우리와 친구가 되고 싶어하신다. 우리가 하는 모든일에 관심이 있으시고, 모든 일 가운데 생기는 고민과 걱정을 함께 나누길 원하신다. 언제 어디서 무엇을 하고 무엇을 먹는지 항상 궁금하시다고 한다. 이 부분을 읽고 나는 아! 하나님이 이렇게 나와 교제하고 싶어하시는데 나는 왜 기도시간에만 기도하고 그랬을까? 라는 생각을 하게 되었고, 앞으로는 수시로 뭘하든지 하나님과 대화하듯이 교제해야겠다고 생각했다. 하나님과 더더욱 교제를 함으로 하나님과 더욱 깊이 친밀해지고 싶다..! 오늘도 열심히 공부하며 나아가자! 망각곡선에 근거한 복습방법으로 공부를 하려고 했는데, 꼭 그렇게 굳이 하지 않아도 된다고 하는 의견도 분분했다. 이 부분은 이 모든 것을 제일 잘 아시는 하나님께 여쭈어봐야 겠다. 할게 너무나 많지만 시간관리를 잘 해서 최선을 다해 주님께 쓰임받기 위한 개발자가 되기 위해 노력하자!
알고리즘
2번까지 복습으로 풀고, 그 이후는 나중에 풀려고 한다. 대신 한문제 한문제 완전히 이해할 수 있을 때까지 풀어보고자 한다.
세그먼트 트리
백준 - 2042번
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
정적 배열에서 구간합을 구하는 경우에는 누적합을 사용하면 되지만, 동적 배열인 경우 + 좀 더 빠른 시간(O(logN))으로 구간합을 구하기 위해선 세그먼트 트리를 사용한다.
세그먼트 트리는 이진트리를 기반으로 각 자식 노드에 절반씩 나눈 구간의 합을 저장해 놓는 것이다.
세그먼트 트리를 사용하려면 우선 3가지 메서드가 필요하다.
(1) 트리를 만드는 메서드
(2) 값이 변경되었을때 구간합을 업데이트 하는 메서드
(3) 주어진 구간의 합을 구하는 메서드
복기한 이 내용을 기반으로, 문제를 다시 풀어보자!
public static long sum(int start, int end, int node, int left, int right) {
if (left > end || right < start) { // 구간을 벗어난 경우
return 0;
}
if (left <= start && right <= end) { // 구간이 겹치거나 내부에 존재하는 경우
return tree[node];
}
// 겹치지 않는 부분이 생기는 경우 => 겹치지 않은 부분에 대한 합을 구해준다.
int mid = (start + end) / 2;
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}
에러가 발생했다..!
스택오버플로우가 났다는 거는 재귀호출이 무한으로 호출되어서 생기는 오류이다.
내가 작성한 sum 함수가 잘못되었다. 어제는 완전히 이해했다고 생각했는데, 아직 완전히 이해하지 못한 것 같다. 어떠한 부분이 잘못되었는지 곰곰히 생각해보자
if (left <= start && right <= end) { // 구간이 겹치거나 내부에 존재하는 경우
return tree[node];
}
이 부분이 잘못된 부분이였다.
구간이 겹치거나 내부에 존재하는 경우를 나타내는 조건문은 다음과 같다.
if(left <= start && end <= right)
주어진 구간은 현재 구간과 겹치거나 클 수 있다.

NumberFormat 에러가 발생했다.
배열을 Long으로 선언하였는데, 막상 값을 넘겨줄때는 int형으로 넘겨주었다. 자료형이 다른 값을 넘겨줌으로 인해 발생하는 문제였다.
선언한 자료형에 맞게 문자열을 올바른 자료형으로 변환시켜 주었다.

엥..? 그래도 틀리는 것이다. 코드를 분석해보자
if (a == 1) { // 수 변경
long dif = c - arr[b]; // 변경된 수가 또 변경될 수 있다.
arr[b] = c;
update(1, N, 1, b, dif);
}
arr[b] = c;이 부분을 빼먹었다. 값을 업데이트하고 업데이트한 값으로 기존 배열의 값을 변경해주어야 한다.
왜냐하면, arr[b]가 단 한번만 변경된다는 가정이 없기 때문이다. 여러번 변경이 될 수 있기 때문에 계속해서 갱신해주어야 한다.
만약 한번만 변경이 되는 것이라면 dif라는 차이값이 주어짐으로 인해 굳이 변경해주지 않아도 된다.
다시 풀기 완료!

원래는 세그먼트 트리를 활용한 문제를 하나 더 풀려고 했지만,
DFS BFS 파트를 복습해보고 싶다는 생각이 들었다. 개념 공부를 복습한 후, 딱 한 문제만 풀어보자
DFS & BFS
개념을 복습해보자!
그래프이론의 기초
정점과 간선
정점(vertex)는 노드라고도 불리며 그래프를 형성하는 기본 단위이다.(점으로 표현되는 위치, 사람, 물건)
간선(Edge)은 정점을 잇는 선을 의미힌다.(관계, 경로)
ex) 어떠한 위치나 어떠한 사람으로부터 무언가를 통해 간다
어떠한 위치나 어떠한 사람 = 정점
무언가를 통해 간다 = 간선
단방향 간선
A라는 사람이 B라는 사람을 좋아한다고 할때, A라는 사람과 B라는 사람은 정점 둘 사이의 마음은 간선이된다.
즉, 단방향 간선은 A라는 사람이 B라는 사람을 좋아하지만, B라는 사람은 A라는 사람을 좋아하지 않는 짝사랑 하는 관계이다.
양방향 간선
A라는 사람도 B라는 사람을 좋아하고, B라는 사람도 A라는 사람을 좋아하는 관계이다.
indegree outdegree
온양온천역(정점 U) <-> 남성역(정점 V)
온양온천역에서 남성역으로 가는 방법은 6개
남성역에서 온양온천역으로 가는 방법은 7개 일때,
온양 온천역의 Outdegree는 6이되고,
남성역의 Indegree는 7이 된다.
정점의 관점에 따라 Outdegree와 Indegree는 달라진다.

정점으로 나가는 간선을 해당 정점의 outdegree라고 하고, 들어오는 간선을 해당 정점의 indegree라고 한다.
정점은 약자로 V또는 U라고 하며 보통 어떤 정점으로부터 시작해서 어떤 정점까지 간다를 "U에서부터 V로 간다"라고 표현을 한다.
그래프란?
정점과 간선의 집합
가중치란?
정점과 정점 사이에 드는 비용을 뜻한다. 1번 노드와 2번 노드까지 가는 비용이 한칸이라면 1번 노드에서 2번 노드까지의 가중치는 한칸이다. ex) 성남이라는 정점에서 네이버라는 정점까지 걸리는 택시비가 13000원이라면 성남에서 네이버까지 가는 가중치는 13000원이 된다.
기본적인 그래프에 대한 개념을 알아보았다. 한번 복습 하고, 문제를 풀어보자!
백준 - 2178번 미로 탐색
https://www.acmicpc.net/problem/2178
2178번: 미로 탐색
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
www.acmicpc.net

나의 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static int N;
public static int M;
public static int[][] map;
public static int[][] visited;
public static int[] dy = {-1, 0, 1, 0};
public static int[] dx = {0, 1, 0, -1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
map = new int[N][M];
visited = new int[N][M];
for (int i = 0; i < N; i++) {
map[i] = Arrays.stream(br.readLine().split("")).mapToInt(Integer::parseInt).toArray();
}
bfs();
System.out.println(visited[N - 1][M - 1]);
}
public static void bfs() {
Queue<Node> queue = new LinkedList<>();
Node node = new Node(0, 0); // 시작지점
queue.add(node);
visited[node.y][node.x] = 1;
while (!queue.isEmpty()) {
Node cur = queue.poll();
for (int i = 0; i < 4; i++) {
int nx = cur.x + dx[i];
int ny = cur.y + dy[i];
if (nx < 0 || nx >= M || ny < 0 || ny >= N) {
continue;
}
if (map[ny][nx] == 1 && visited[ny][nx] == 0) { // 이동할 수 있고, 방문을 하지 않은 경우
visited[ny][nx] = visited[cur.y][cur.x] + 1; // 한개 증가시켜준다.
queue.add(new Node(ny, nx));
}
}
}
}
public static class Node {
int y;
int x;
public Node(int y, int x) {
this.x = x;
this.y = y;
}
}
}
(1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수
최소의 칸 수를 보자마자 바로 BFS를 떠올렸다.
visited 이차원 배열에 이동 횟수를 누적해주는 방식으로 구현을 해 주었다.
강의 해설
가중치가 다른 경우에는 최단거리 알고리즘, 다익스트라, 플루이드 워셜 알고리즘을 사용해야 하지만, 가중치가 같은 경우의 최단거리를 구할려면 BFS를 사용해주어야 한다.
BFS & DFS를 한 문제만 더 풀어보자!
백준 - 1012번 유기농 배추
https://www.acmicpc.net/problem/1012
1012번: 유기농 배추
차세대 영농인 한나는 강원도 고랭지에서 유기농 배추를 재배하기로 하였다. 농약을 쓰지 않고 배추를 재배하려면 배추를 해충으로부터 보호하는 것이 중요하기 때문에, 한나는 해충 방지에
www.acmicpc.net

문제 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static int T;
public static int M;
public static int N;
public static int K;
public static int[][] map;
public static boolean[][] visited;
public static int[] dy = {-1, 0, 1, 0};
public static int[] dx = {0, 1, 0, -1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
T = Integer.parseInt(br.readLine());
for (int i = 0; i < T; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
M = Integer.parseInt(st.nextToken()); // 세로 길이
N = Integer.parseInt(st.nextToken()); // 가로 길이
K = Integer.parseInt(st.nextToken()); // 위치의 갯수
// 초기화
map = new int[M][N];
visited = new boolean[M][N];
int count = 0;
for (int j = 0; j < K; j++) { // 초기화
st = new StringTokenizer(br.readLine());
int y = Integer.parseInt(st.nextToken());
int x = Integer.parseInt(st.nextToken());
map[y][x] = 1;
}
for (int j = 0; j < M; j++) {
for (int k = 0; k < N; k++) {
if (!visited[j][k] && map[j][k] == 1) { // 방문하지 않은 곳
dfs(j, k);
count++; // dfs 탈출 하면 카운터 증가
}
}
}
System.out.println(count);
}
}
public static void dfs(int y, int x) {
visited[y][x] = true;
for (int i = 0; i < 4; i++) {
int ny = y + dy[i];
int nx = x + dx[i];
if (ny < 0 || ny >= M || nx < 0 || nx >= N) {
continue;
}
if (map[ny][nx] == 1 && !visited[ny][nx]) {
dfs(ny, nx); // 깊이 우선 탐색
}
}
}
}
오예~~! 맞았다!
인접한 배추는 모조리 탐색을 하기 위해 dfs(깊이 우선 탐색)을 사용해주었다. dfs가 탈출하는 순간은 바로 인접한 배추가 없다는 소리이므로, 벌레를 한마리 추가해주어야 한다.
이 문제에서 시간이 좀 걸렸던 이유는 주어진 Map의 가로,세로를 구분하는게 헷갈렸고, 배추인 곳을 기점으로 탐색을 해야하는데 전부다 탐색을 하고 있었다... 생각을 좀 더 깊이하고, 문제를 풀어나가는 자세를 갖도록 하자!
최단거리를 한번 풀어보고 싶다! 가중치가 다를때 사용되는 최단거리 알고리즘을 풀어보고 싶다!
최단거리
주어진 그래프에서 두 정정을 연결하는 가장 짧은 경로의 길이를 찾는, 경로에 포함되는 정점들을 찾는 문제
가중치가 다르다? BFS말고 최단거리 알고리즘 사용
최단거리는 주어진 그래프에서 두 정점을 연결하는 가장 짧은 경로의 길이를 찾는 경로에 포함되는 정점들을 찾는 문제이다.
BFS는 가중치가 같은 그래프에서 최단거리 알고리즘으로 올 수 있고, 가중치가 다를 경우 최단거리 알고리즘을 써야 한다.
최단거리는 다익스트라, 벨만 포드, 플로이드워셜 알고리즘이 있고, 이들 모두 DP의 일종이다. 최적의 배열을 하나 만드는 것에 불과하다.
다익스트라
(1) 음의 가중치가 없는 그래프에서 사용할 수 있으며
(2) 우선순위큐에 PQ에 있는 정점에서 해당 정점까지의 거리가 가장 낮은 정점을 중심으로 거리 배열을 갱신하여 다시 큐에 넣는 행위를 반복하여 최종적으로 거리배열을 완성하는 알고리즘
(3) 정점 v까지 거리와 비교하여 더 짧아진 경우 갱신한다. dist[u] + w(u,v) = dist[v]로 갱신한다는 것이다. 이때 갱신이 일어났을 때를 완화가 일어났다고 한다.
다익스트라 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로 탐색 알고리즘이다. 인공위성 GPS 소프트웨어 등에서 가장 많이 사용된다. 다익스트라 알고리즘은 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려준다. 이때 음의 간선을 포함할 수 없다.
다익스트라 알고리즘이 다이나믹 프로그래밍 문제인 이유는 최단 거리는 여러 개의 최단 거리로 이루어져있기 때문입니다.
작은 문제가 큰 문제의 부분 집합에 속해있다고 볼 수 있다. 기본적으로 다익스트라는 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단거리의 정보를 그대로 사용한다는 특징이 있다.
1부터 다른 모든 노드로 가는 최단 경로를 구해야 한다.

1에 당장 붙어있는 노드인 2,3,4까지의 최단 거리를 각각 3,6,7로 산정할 수 있다.

이후에 다음 노드인 2를 처리하게 되었다고 가정해보자.
경로 1->3의 비용이 6인데 반해 경로 1->2->3의 비용은 4로 더 저렴하다는 것을 알게 된다.
이 때 현재까지 알고 있던 3으로 가는 최소 비용 6을 새롭게 4로 갱신한다.
다익스트라 알고리즘은 현재까지 알고 있던 최단 경로를 계속해서 갱신 한다.
작동 과정
(1) 출발 노드를 설정한다.
(2) 출발 노드를 기준으로 각 노드의 최소 비용을 저장한다.
(3) 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택한다.
(4) 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신한다.
(5) 3번 ~ 4번을 반복한다.
예시로 확인해보기
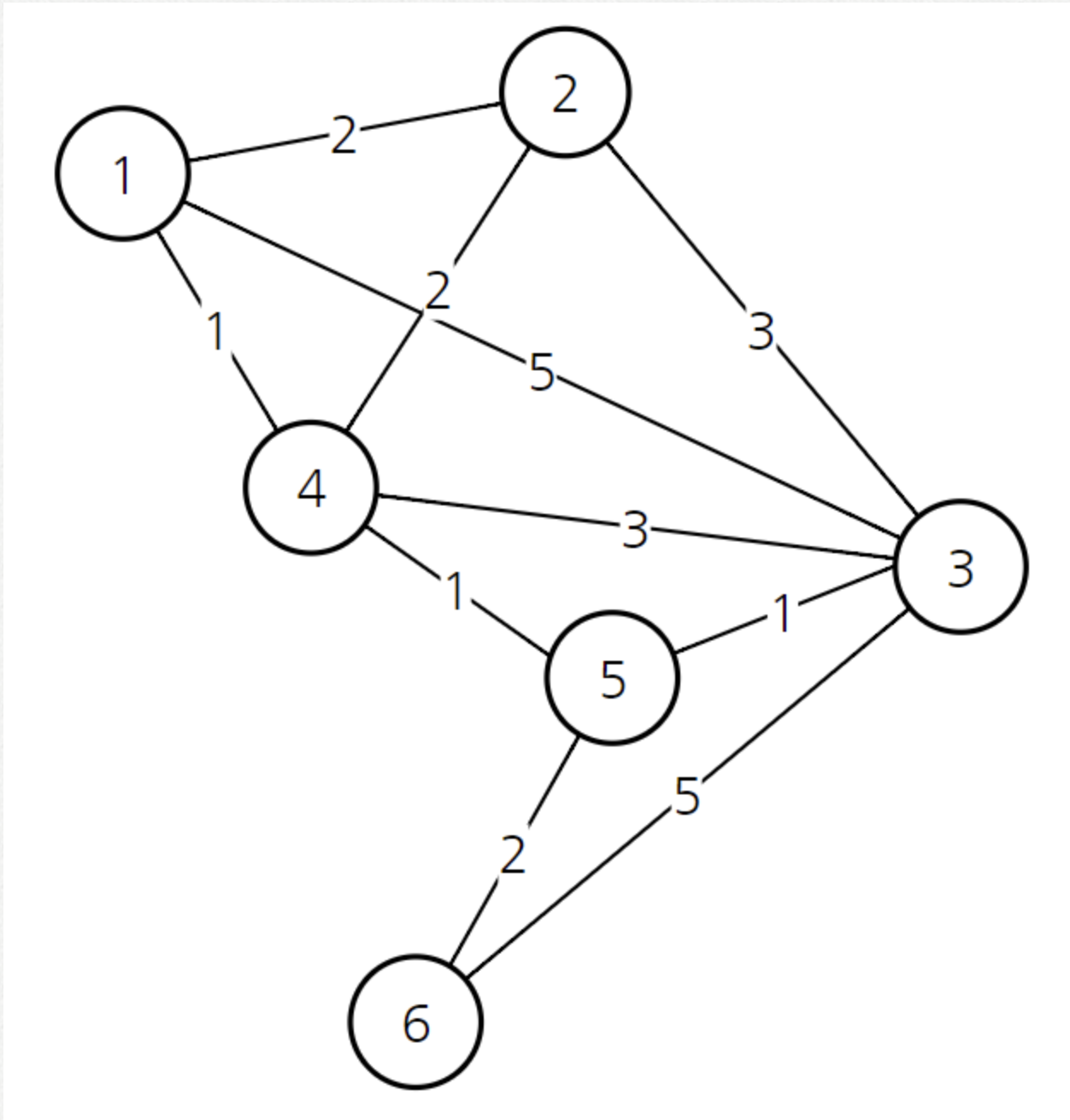
이러한 그래프는 실제로 컴퓨터 안에서 처리할 때 이차원 배열 형태로 처리해야 한다.

1번 노드에서 3번 노드로 가는 비용이 5
1행 3열의 값 : 5
이 상태에서 1번 노드를 선택한다.

노드 1을 선택한 상태고, 그와 연결된 3개의 간선을 확인한 상태이다.
1번 노드에서 다른 정점으로 가는 최소 비용은 다음과 같다. 배열을 만든 뒤에는 이 최소 비용 배열을 계속해서
갱신할 것이다. 현재 방문하지 않은 노드 중에서 가장 비용이 적은 노드는 4번 노드이다.

위 배열 상태를 고려하여 비용이 가장 적은 노드인 4번 노드가 선택되었다. 4번 노드를 거쳐서 가는 경우를 모두 고려하여 최소 비용 배열을 갱신하면 된다.

기존에 5로 가는 최소 비용은 무한이였다. 하지만 4를 거쳐서 5로 가는 경우 비용이 2이므로 최소 비용 배열을 갱신해준다.
또한 4를 거쳐서 3으로 가는 비용이 4이므로 기존보다 더 저렴하다. 따라서 최소 비용 배열을 갱신해준다.

(노란색은 방문한 노드)
다음으로 방문하지 않은 노드 중에서 가장 비용이 적은 노드는 2번 노드이다.
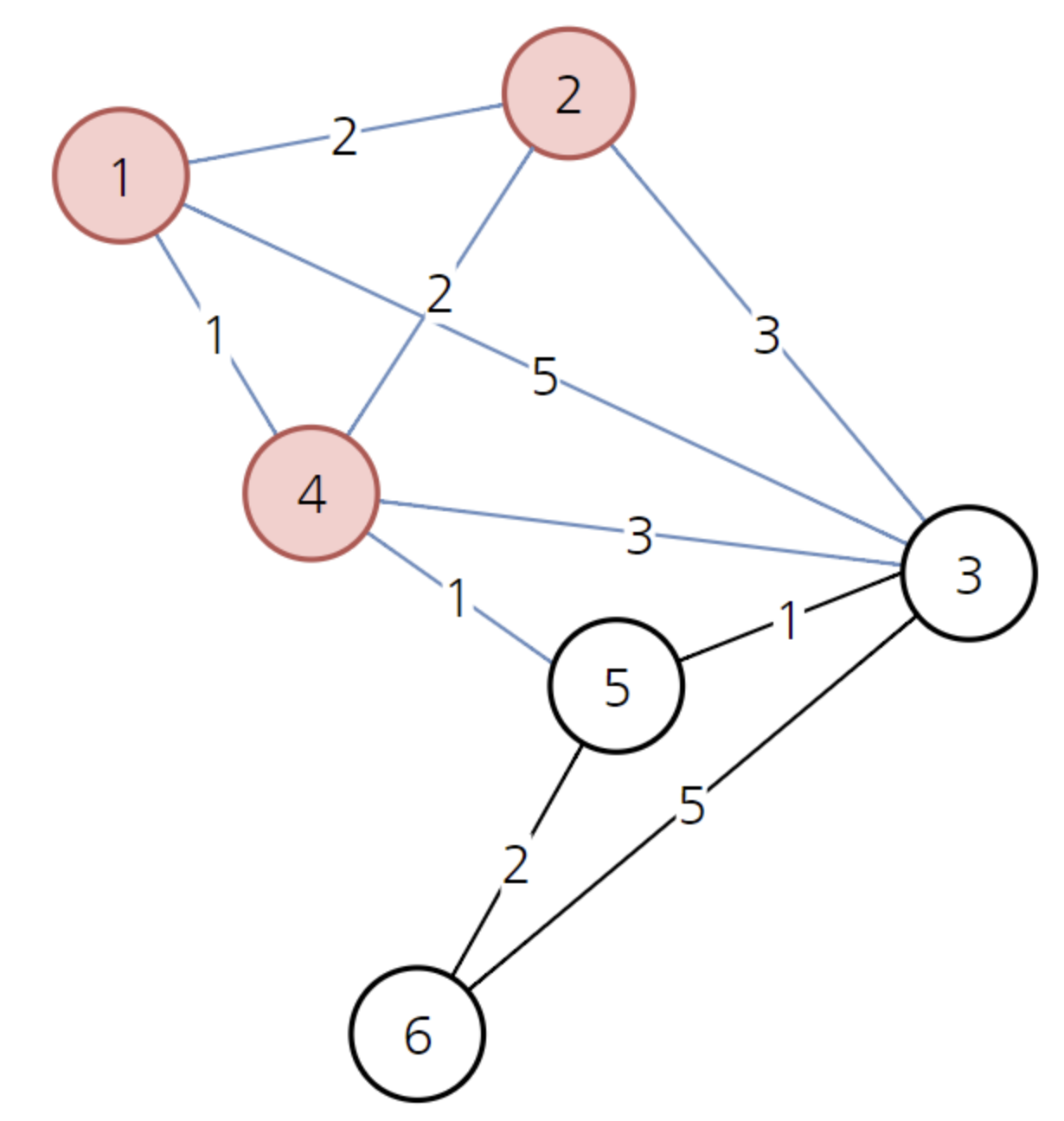
2를 거쳐서 가더라도 비용이 갱신되는 경우가 없다. 배열은 그대로 유지한다.

다음으로 방문하지 않은 노드 중에서 가장 비용이 적은 노드는 5번째 노드이다.

5를 거쳐서 3으로 가는 경우 경로의 비용이 3이므로 기존의 4보다 더 저렴하다.
따라서 노드 3으로 가는 비용을 3으로 바꿔주면 된다. 또한 5를 거쳐서 6으로 가는 경우 경로의 비용이 4로 기존의 무한보다 더 저렴하다.
따라서 노드 6으로 가는 비용을 4로 바꾸어주면 된다.

이후에 방문하지 않은 노드 중에서 가장 저렴한 노드 3을 방문한다.

최소 비용 갱신은 일어나지 않는다.

마지막으로 남은 노드6을 살펴 보자

노드 6을 방문한 뒤에도 결과는 같다. 최종 배열은 다음과 같이 형성된다.

최소 비용을 선형 탐색으로 찾는 경우 다익스트라의 시간 복잡도가 O(N^2)으로 형성된다. 최대한 빠르게 작동시켜야 하는 경우 힙 구조를 황용하여 시간 복잡도 O(N * logN)을 만들 수 있다.
백준 - 1753 최단경로
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
다익스트라 알고리즘을 한번도 사용해보지 않아서..
다른 사람의 풀이를 보고 코드를 분석했다.

풀이 코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
private static final int INF = 100_000_000;
public static int v, e, k;
public static List<Node>[] list;
public static int[] dist;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
v = Integer.parseInt(st.nextToken());
e = Integer.parseInt(st.nextToken());
k = Integer.parseInt(br.readLine());
list = new ArrayList[v + 1];
dist = new int[v + 1];
Arrays.fill(dist, INF); // INF로 채우기
for (int i = 1; i <= v; i++) { // 간선 채우기
list[i] = new ArrayList<>();
}
// 그래프 정보 초기화
for (int i = 0; i < e; i++) { // 간선 갯수
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// start -> end 가중치
list[start].add(new Node(end, weight));
}
StringBuilder sb = new StringBuilder();
dijkstra(k);
for (int i = 1; i <= v; i++) {
if (dist[i] == INF) {
sb.append("INF\n");
} else {
sb.append(dist[i] + "\n");
}
}
bw.write(sb.toString());
bw.flush();
br.close();
bw.close();
}
private static void dijkstra(int start) {
PriorityQueue<Node> queue = new PriorityQueue<>();
boolean[] check = new boolean[v + 1];
queue.add(new Node(start, 0)); // 시작지점 가중치 0
dist[start] = 0;
while (!queue.isEmpty()) {
Node curNode = queue.poll(); // 제일 거리가 짧은 노드
int cur = curNode.end;
if (check[cur] == true) { // 이미 방문을 했다면
continue;
}
check[cur] = true; // 방문 처리 해주고
for (Node node : list[cur]) { // cur에 연결된 노드들 방문하고
if (dist[node.end] > dist[cur] + node.weight) { // 거리가 더 짧으면!
dist[node.end] = dist[cur] + node.weight; // 거리가 더 짧은 값으로 갱신
queue.add(new Node(node.end, dist[node.end])); // 가중치 이전 값으로 누적 -> 우선순위 큐에서 알아서 가중치가 적은 노드를 가져와준다.
}
}
}
}
// 우선순위큐를 사용하기 위한 Comparable 인터페이스를 추가해준다.
public static class Node implements Comparable<Node> { // Comparable : 객체간 값 비교
int end, weight;
public Node(int end, int weight) {
this.end = end;
this.weight = weight;
}
@Override
public int compareTo(Node o) { // 가중치를 기준으로 정렬
return weight - o.weight;
}
}
}
우선순위 큐를 사용해 힙 구조로 인해 시간 복잡도가 O(N * logN)이 된다.
객체를 이용한 우선순위 큐를 사용하기 위해서는 사용되는 객체에 Comparable 인터페이스를 구현해주어야 한다.
알고리즘 자체를 구현하는 코드는 어느정도 이해를 했다. 알고리즘 공부는 오늘 여기까지 하자.
Spring
스프링은 오늘 졸업작품을 제작하는데 시간을 소요했다.
이제 졸업작품하면서 막히는 부분이나 공부하는 부분을 기록하자!
cs공부를 미루고 미루다가 이제 한다.
오늘부터 1시간씩 공부하자!
CS
운영체제란?
OS(Operating System)
주요 운영체제: 윈도우, UNIX 계열 OS(리눅스), MacOS
사용자, 응용 프로그램, 운영체제, 컴퓨터 하드웨어 관계
- OS는 더 정확히는 커널(kernel)을 의미함

일반적으로는 커널에 여러가지가 추가된 상태를, OS라고 통칭한다.
안드로이드는 OS 인가?
안드로이드는 OS가 아니다!

안드로이드는 운영체제가 아니라 그 안에 리눅스(커널)가 들어가 있다.
그 위에서 안드로이드용 앱이 동작하기 위한 여러가지 구성요소들이 있다.
kernel과 프로그램 사이에 많은 시스템 프로그램과 함수(라이브러리)들이 존재한다.
운영체제는 사용자 인터페이스 제공 : 쉘
쉘(Shell)
- 사용자가 운영체제 기능과 서비스를 조작할 수 있도록 인터페이스를 제공하는 프로그램
- 쉘은 터미널 환경(CLI)과 GUI 환경 두 종류로 분류
- 유명한 쉘 : 리눅스 bash
커널 위에서 동작하는 일종의 응용프로그램

시스템 콜(System Call)
- 시스템 콜 또는 시스템 호출 인터페이스
- 운영체제가 운영체제 각 기능을 사용할 수 있도록 시스템 콜이라는 명령 또는 함수를 제공
- 쉘에서 커널에 요청이 필요할 경우 시스템 콜(함수 형태) 인터페이스를 사용해서 요청한다.
프로그래밍 언어별 해당 운영체제에 맞는 API 구현
- API(Application Programming interface)
- API 내부에는 필요시 해당 운영체제의 시스템콜을 호출하는 형태로 만들어짐

만약 운영체제를 만든다면?
(1) 운영체제를 개발한다 (kernel)
(2) 시스템콜을 개발
(3) 시스템콜 기반, 프로그래밍 언어별 라이브러리 개발(API)
(4) 지원되는 프로그래밍 언어로 Shell 프로그램 개발
(5) 지원되는 프로그래밍 언어로 응용 프로그램 개발
Java 언어로 작성하면 왜 OS 별로 만들지 않아도 되는가?
JAVA 프로그램 동작을 위해, JRE(JDK) 설치가 필요한 이유
JDK : JAVA의 코드를 각각의 운영체제에 동작을 할 수 있게끔 처리를 해준다.
사용자 모드와 커널 모드
함부로 응용 프로그램이 전체 컴퓨터 시스템을 해치지 못함
주민등록본은 꼭 동사무소 또는 민원24시(정부 사이트)에서 특별한 신청서를 써야만, 발급
'Backend > 공부 일지' 카테고리의 다른 글
| 2024/03/28(목) (1) | 2024.03.29 |
|---|---|
| 2024/03/27(수) (1) | 2024.03.27 |
| 2024/03/12(화) (0) | 2024.03.13 |
| 2024/03/11(월) (2) | 2024.03.12 |
| 2024/03/05(화) 가자! 네카라쿠배당토 (0) | 2024.03.05 |

